If you have a large number of training features, theoretically, it should improve performance of your model. However, in practice, you can encounter curse of dimensionality because number of training examples required increases exponentially with dimensionality.
It's pretty clear that we need to reduce the complexity of our input training data so that it has fewer dimensions, but how do we go about doing it?
Now, complexity in your training data can be reduced using techniques in two broad categories, feature selection and dimensionality reduction. Within feature selection, you can apply statistical techniques to select the most significant features in your dataset. Examples of statistical techniques that you could use here are variance thresholding, ANOVA, and mutual information.
There are of course, many others as well. Dimensionality reduction involves transforming the data so that most of the information in the original dataset is preserved, but with fewer dimensions. There are three categories of techniques that you can use for dimensionality reduction, projection, manifold learning, and autoencoding
In this post, we will focus one of popular and efficient techniques which works well with linear data: Principal Component Analysis.
Principal Component Analysis (PCA)
Let's first focus our attention on understanding the intuition behind principal component:
- We have 2 features: height and cigarettes per day
- Both features increase together (correlated)
Do we really need two dimensions to represent this data? Can we reduce number of features to one?
The answer is to create single feature that is combination of height and cigarettes
Choice 1: Let's say we choose to project all of your points along this X axis. This is a bad choice of dimensions! If we choose our axes or dimensions poorly, then we do need two dimensions to represent this data. By projecting onto the X axis, we've lost all of the information present in the original set of points.
 |
| Project data-points to X axis |
Choice 2: What if we project all of these points onto the Y axis? Observe now that the distances between the original points are preserved. If we choose our axes or dimensions well, then one dimension is sufficient to represent this data. Observe here that the right choice of dimensions allows us to represent the same set of points in lower dimensionality.
Intuition Behind PCA
Now our objective here is to find the "best" direction to represent this data. what do we consider the best direction? How many directions are good enough to express the original data?
From the earlier example, a good projection is where the distances between points are maximized. The distances between points, which can be thought of as the variance in the original data.
The direction along which this variance is maximized is the best possible direction, and this is the first principal component
Now there are of course other principal components. Draw a line which is at right angles, or at 90 degrees to the first one, and this will be the second principal component.
It represents the original set of data points must be at right angles to the first and captures less variation in the data as compared with the first.
Why at 90 degrees to the first principal component you might ask?
Well, directions at right angles help express the most variation in the underlying data with the smallest number of directions.
In general, we can have as many principal components as there are dimensions in the original data. Two-dimensional data will have two principal components. N-dimensional data will have N principal components. Once we've figured out the best axes to represent this data, we can then reorient all of the original data points along these new axes. So all of the original points will be re-expressed in terms of these principal components
Importance of Feature Scaling
PCA seek to find the vectors that capture the most variance so that variance is sensitive to axis scale. For that reason, data must be normalized and transformed (scaled, outliers removed) before applying PCA
Implement PCA With Real Dataset
I want to analyze customers’ interaction throughout the customer journey so that I'm enable to learn something about customers and thereby improve marketing opportunities and purchase rates.One goal of the project is to describe the variation in the different types of customers that a wholesale distributor interacts with and to predict dynamically segmentation so that I can design campaigns, creatives and schedule for product release
Know Your Data
Data Source
Data Structure
- Fresh: annual spending (m.u.) on fresh products (Continuous);
- Milk: annual spending (m.u.) on milk products (Continuous);
- Grocery: annual spending (m.u.) on grocery products (Continuous);
- Frozen: annual spending (m.u.) on frozen products (Continuous);
- Detergents_Paper: annual spending (m.u.) on detergents and paper products (Continuous);
- Delicatessen: annual spending (m.u.) on and delicatessen products (Continuous);
- Channel: {Hotel/Restaurant/Cafe - 1, Retail - 2} (Nominal)
- Region: {Lisnon - 1, Oporto - 2, or Other - 3} (Nominal)
Data Distribution
As we can see, Fresh is largely distributed in Hotel/Restaurant/Cafe meanwhile Grocery is highly proportioned in distribution of Retail, following is Milk, Fresh and Detergents_Paper products.
However, both channels sold very few Delicatessen and Frozen products.
Is there any degree of correlation of pairs of feature? In another words, can sale of one product impacted to others? Is the data distributed normal?
- To get a better understanding of the dataset, we can construct a scatter matrix of each of the six product features present in the data. If you found that the feature you attempted to predict above is relevant for identifying a specific customer, then the scatter matrix below may not show any correlation between that feature and the others.
- Conversely, if you believe that feature is not relevant for identifying a specific customer, the scatter matrix might show a correlation between that feature and another feature in the data
From the scatter matrix, it can be observed that that the pair (Grocery, Detergents_Paper) seems to have the strongest correlation. The pair (Grocery, Milk) and (Detergents_Paper, Milk) also seem to exhibit some degree of correlation. This scatter matrix also confirms my initial suspicions that Fresh, Frozen and Delicatessen product category don't have significant correlations to any of the remaining features.
Additionally, this scatter matrix also show us that the data for these features is highly skewed and not normally distributed.
Data Pre-processing
Data Normalization
As we can see from scatter plot, the data is left skewed and statistically, mean and standard deviation significantly vary. We have to rescale data before moving to further steps. There are some ways to achieve this scaling such as natural logarithm or Box-Cox test.
In this project, I will use Box-Cox test implemented from scipy.stats.boxcox. The Box Cox transformation is used to stabilize the variance (eliminate heteroskedasticity) and also to (multi)normalize a distribution. We shall observe the transformed data again in scatter plot to see how well it is rescaled.
After applying a Box-Cox scaling to the data, the distribution of each feature should appear much more normal. For any pairs of features we may have identified earlier as still being correlated.
Lets look at the mean and variance after the normalization:
Mean and standard deviation are reduced after normalization and data distribution is less skewed than before. It seems we are doing the right thing !!!
Outliers Detection
Anomalies, or outliers, can be a serious issue when training machine learning algorithms or applying statistical techniques. They are often the result of errors in measurements or exceptional system conditions and therefore do not describe the common functioning of the underlying system. Indeed, the best practice is to implement an outlier removal phase before proceeding with further analysis.
There are many techniques to detect and optionally remove outliers: Numeric Outlier, Z-Score, DBSCAN.
- Numeric Outlier: This is the simplest, nonparametric outlier detection method in a one dimensional feature space. Outliers are calculated by means of the IQR (InterQuartile Range) with interquartile multiplier value k=1.5.
- Z-score: is a parametric outlier detection method in a one or low dimensional feature space. This technique assumes a Gaussian distribution of the data. The outliers are the data points that are in the tails of the distribution and therefore far from the mean
- DBSCAN: This technique is based on the DBSCAN clustering method. It is a non-parametric, density based outlier detection method in a one or multi dimensional feature space. This is a non-parametric method for large datasets in a one or multi dimensional feature space
In this project, I will go with Numeric Outlier method because it is simple and it can work well because data is already transformed. To implement Numeric Outlier, we have to:
- Assign the value of the 25th percentile for the given feature to Q1. Use np.percentile for this.
- Assign the value of the 75th percentile for the given feature to Q3. Again, use np.percentile.
- Assign the calculation of an outlier step for the given feature to step.
- Optionally remove data points from the dataset by adding indices to the outliers list.
Most of outliers dropped come from Delicatessen and Frozen meanwhile Detergent_papers feature has not data points considered as outliers after applying boxcox transformation.
Feature Relevance
One interesting thought to consider is if one (or more) of the six product categories is actually relevant for understanding customer purchasing. That is to say, is it possible to determine whether customers purchasing some amount of one category of products will necessarily purchase some proportional amount of another category of products? We can make this determination quite easily by training a supervised regression learner on a subset of the data with one feature removed, and then score how well that model can predict the removed feature.
Using DecisionTreeRegressor to predict which feature is most relevant to be target variable. Based one mean squared error (the smaller, the better) score returned from regressor, we can probably guess the relevant feature is the one with lowest positive score
What does the Mean Squared Error (mse) tell you?
The smaller the means squared error, the closer you are to finding the line of best fit. Negative scores means the feature fails to be predicted.
Delicatessen & Fresh & Frozen can't be considered as target variable. If i was asked to choose a feature as predicted variable, I would say it is Detergents_Paper which lowerest positive score is Detergents_Paper , which should be most relevant feature in dataset
Feature Transformation - PCA
Now we are done with data processing. We shall use PCA (Principal Components Analysis) in sklearn to extract the important features in the dataset. When using principal component analysis, one of the main goals is to reduce the dimensionality of the data — in effect, reducing the complexity of the problem. Dimensionality reduction comes at a cost: Fewer dimensions used implies less of the total variance in the data is being explained.
After transforming data, we shall plot new data along with explained variance ratio of each component in bar chart
The plot above clearly shows that most of the variance (87.48% of the variance to be precise) can be explained by the first principal component alone. The second principal component still bears some information (6.79%) while the third, fourth, fifth and sixth principal components can safely be dropped without losing to much information. Together, the first two principal components contain 94.27% of the information.
Data Scaling and Dimensionality Reduction
We will biplot data again with 2 principal components in in 2D scatterplot where each datapoint is represented by its scores along the principal components. In addition, the biplot shows the projection of the original features along the components. A biplot can help us interpret the reduced dimensions of the data, and discover relationships between the principal components and original features.
Prior to PCA, it makes sense to standardize the data, especially, if it was measured on different scales.
There is high correlation in spending of clients who buy Frozen and Fresh products. However, clients who buy Grocery products who will buy Detergents_Paper and Milk products. Delicatessen seems unrelated to other products.
Clustering with Agglomerative Clustering
Agglomerative Clustering algorithm groups similar objects into groups called clusters. It recursively merges the pair of clusters that minimally increases a given linkage distance. It starts with many small clusters and merge them together to create bigger clusters.
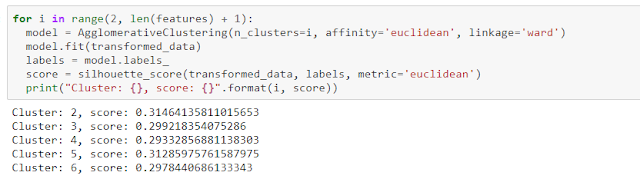
What is the number of cluster to be considered as a good parameter to algorithm for this case? Using sklearn.metrics.silhouette_score to calculate the distance between features and clusters. We choose the value with the highest score
Clearly, Model returns the highest score with cluster=2. Fitting model with data which is transformed and plotting clustered data






















No comments:
Post a Comment