Dimensionality Reduction with Principal Component Analysis

If you have a large number of training features, theoretically, it should improve performance of your model.  However, in practice, you can encounter curse of dimensionality because number of training examples required increases exponentially with dimensionality.

It's pretty clear that we need to reduce the complexity of our input training data so that it has fewer dimensions, but how do we go about doing it? 

Now, complexity in your training data can be reduced using techniques in two broad categories, feature selection and dimensionality reduction. Within feature selection, you can apply statistical techniques to select the most significant features in your dataset. Examples of statistical techniques that you could use here are variance thresholding, ANOVA, and mutual information. 

There are of course, many others as well. Dimensionality reduction involves transforming the data so that most of the information in the original dataset is preserved, but with fewer dimensions. There are three categories of techniques that you can use for dimensionality reduction, projection, manifold learning, and autoencoding

In this post, we will focus one of popular and efficient techniques which works well with linear data: Principal Component Analysis.

Principal Component Analysis (PCA)

Let's first focus our attention on understanding the intuition behind principal component:

• We have 2 features: height and cigarettes per day 
• Both features increase together (correlated) 

Do we really need two dimensions to represent this data? Can we reduce number of features to one?

The answer is to create single feature that is combination of height and cigarettes

Project data-points to Y axis

Choice 1: Let's say we choose to project all of your points along this X axis. This is a bad choice of dimensions! If we choose our axes or dimensions poorly, then we do need two dimensions to represent this data. By projecting onto the X axis, we've lost all of the information present in the original set of points.

Project data-points to X axis

Choice 2: What if we project all of these points onto the Y axis? Observe now that the distances between the original points are preserved. If we choose our axes or dimensions well, then one dimension is sufficient to represent this data. Observe here that the right choice of dimensions allows us to represent the same set of points in lower dimensionality.

Intuition Behind PCA

Now our objective here is to find the "best" direction to represent this data. what do we consider the best direction? How many directions are good enough to express the original data?

From the earlier example, a good projection is where the distances between points are maximized. The distances between points, which can be thought of as the variance in the original data. 

The direction along which this variance is maximized is the best possible direction, and this is the first principal component

Now there are of course other principal components. Draw a line which is at right angles, or at 90 degrees to the first one, and this will be the second principal component. 

It represents the original set of data points must be at right angles to the first and captures less variation in the data as compared with the first.

Why at 90 degrees to the first principal component you might ask? 

Well, directions at right angles help express the most variation in the underlying data with the smallest number of directions. 

In general, we can have as many principal components as there are dimensions in the original data. Two-dimensional data will have two principal components. N-dimensional data will have N principal components. Once we've figured out the best axes to represent this data, we can then reorient all of the original data points along these new axes. So all of the original points will be re-expressed in terms of these principal components

Importance of Feature Scaling

PCA seek to find the vectors that capture the most variance so that variance is sensitive to axis scale. For that reason, data must be normalized and transformed (scaled, outliers removed) before applying PCA

Implement PCA With Real Dataset

I want to analyze customers’ interaction throughout the customer journey so that I'm enable to learn something about customers and thereby improve marketing opportunities and purchase rates.

One goal of the project is to describe the variation in the different types of customers that a wholesale distributor interacts with and to predict dynamically segmentation so that I can design campaigns, creatives and schedule for product release

Know Your Data

Data Source

The customer segments data is included as a selection of 440 data points collected on data found from clients of a wholesale distributor in Lisbon, Portugal. More information can be found on UCI Machine Learning Repository

Data Structure

• Fresh: annual spending (m.u.) on fresh products (Continuous);
• Milk: annual spending (m.u.) on milk products (Continuous);
• Grocery: annual spending (m.u.) on grocery products (Continuous);
• Frozen: annual spending (m.u.) on frozen products (Continuous);
• Detergents_Paper: annual spending (m.u.) on detergents and paper products (Continuous);
• Delicatessen: annual spending (m.u.) on and delicatessen products (Continuous);
• Channel: {Hotel/Restaurant/Cafe - 1, Retail - 2} (Nominal)
• Region: {Lisnon - 1, Oporto - 2, or Other - 3} (Nominal)

Data Distribution

The mean & standard deviation are high among features. We can probably guess that data is noisy and skewed.

How are sales of product distributed in channels?

As we can see, Fresh is largely distributed in Hotel/Restaurant/Cafe meanwhile Grocery is highly proportioned in distribution of Retail, following is Milk, Fresh and Detergents_Paper products. 

However, both channels sold very few Delicatessen and Frozen products.

Is there any degree of correlation of pairs of feature? In another words, can sale of one product impacted to others? Is the data distributed normal?

• To get a better understanding of the dataset, we can construct a scatter matrix of each of the six product features present in the data. If you found that the feature you attempted to predict above is relevant for identifying a specific customer, then the scatter matrix below may not show any correlation between that feature and the others.
• Conversely, if you believe that feature is not relevant for identifying a specific customer, the scatter matrix might show a correlation between that feature and another feature in the data

From the scatter matrix, it can be observed that that the pair (Grocery, Detergents_Paper) seems to have the strongest correlation. The pair (Grocery, Milk) and (Detergents_Paper, Milk) also seem to exhibit some degree of correlation. This scatter matrix also confirms my initial suspicions that Fresh, Frozen and Delicatessen product category don't have significant correlations to any of the remaining features.

Additionally, this scatter matrix also show us that the data for these features is highly skewed and not normally distributed.

Data Pre-processing

Data Normalization

As we can see from scatter plot, the data is left skewed and statistically, mean and standard deviation significantly vary. We have to rescale data before moving to further steps. There are some ways to achieve this scaling such as natural logarithm or Box-Cox test. 

In this project, I will use Box-Cox test implemented from scipy.stats.boxcox. The Box Cox transformation is used to stabilize the variance (eliminate heteroskedasticity) and also to (multi)normalize a distribution. We shall observe the transformed data again in scatter plot to see how well it is rescaled.

After applying a Box-Cox scaling to the data, the distribution of each feature should appear much more normal. For any pairs of features we may have identified earlier as still being correlated.

Lets look at the mean and variance after the normalization:

Mean and standard deviation are reduced after normalization and data distribution is less skewed than before. It seems we are doing the right thing !!!

Outliers Detection

Anomalies, or outliers, can be a serious issue when training machine learning algorithms or applying statistical techniques. They are often the result of errors in measurements or exceptional system conditions and therefore do not describe the common functioning of the underlying system. Indeed, the best practice is to implement an outlier removal phase before proceeding with further analysis.

There are many techniques to detect and optionally remove outliers: Numeric Outlier, Z-Score, DBSCAN.

• Numeric Outlier: This is the simplest, nonparametric outlier detection method in a one dimensional feature space. Outliers are calculated by means of the IQR (InterQuartile Range) with interquartile multiplier value k=1.5.
• Z-score: is a parametric outlier detection method in a one or low dimensional feature space. This technique assumes a Gaussian distribution of the data. The outliers are the data points that are in the tails of the distribution and therefore far from the mean
• DBSCAN: This technique is based on the DBSCAN clustering method. It is a non-parametric, density based outlier detection method in a one or multi dimensional feature space. This is a non-parametric method for large datasets in a one or multi dimensional feature space

In this project, I will go with Numeric Outlier method because it is simple and it can work well because data is already transformed. To implement Numeric Outlier, we have to:

• Assign the value of the 25th percentile for the given feature to Q1. Use np.percentile for this.
• Assign the value of the 75th percentile for the given feature to Q3. Again, use np.percentile.
• Assign the calculation of an outlier step for the given feature to step.
• Optionally remove data points from the dataset by adding indices to the outliers list.

Most of outliers dropped come from Delicatessen and Frozen meanwhile Detergent_papers feature has not data points considered as outliers after applying boxcox transformation.

Feature Relevance

One interesting thought to consider is if one (or more) of the six product categories is actually relevant for understanding customer purchasing. That is to say, is it possible to determine whether customers purchasing some amount of one category of products will necessarily purchase some proportional amount of another category of products? We can make this determination quite easily by training a supervised regression learner on a subset of the data with one feature removed, and then score how well that model can predict the removed feature.

Using DecisionTreeRegressor to predict which feature is most relevant to be target variable. Based one mean squared error (the smaller, the better) score returned from regressor, we can probably guess the relevant feature is the one with lowest positive score

What does the Mean Squared Error (mse) tell you?

The smaller the means squared error, the closer you are to finding the line of best fit. Negative scores means the feature fails to be predicted. 

Delicatessen & Fresh & Frozen can't be considered as target variable. If i was asked to choose a feature as predicted variable, I would say it is Detergents_Paper which lowerest positive score is Detergents_Paper , which should be most relevant feature in dataset

Feature Transformation - PCA

Now we are done with data processing. We shall use PCA (Principal Components Analysis) in sklearn to extract the important features in the dataset. When using principal component analysis, one of the main goals is to reduce the dimensionality of the data — in effect, reducing the complexity of the problem. Dimensionality reduction comes at a cost: Fewer dimensions used implies less of the total variance in the data is being explained.

After transforming data, we shall plot new data along with explained variance ratio of each component in bar chart

The plot above clearly shows that most of the variance (87.48% of the variance to be precise) can be explained by the first principal component alone. The second principal component still bears some information (6.79%) while the third, fourth, fifth and sixth principal components can safely be dropped without losing to much information. Together, the first two principal components contain 94.27% of the information.

Data Scaling and Dimensionality Reduction

We will biplot data again with 2 principal components in in 2D scatterplot where each datapoint is represented by its scores along the principal components. In addition, the biplot shows the projection of the original features along the components. A biplot can help us interpret the reduced dimensions of the data, and discover relationships between the principal components and original features.

Prior to PCA, it makes sense to standardize the data, especially, if it was measured on different scales.

There is high correlation in spending of clients who buy Frozen and Fresh products. However, clients who buy Grocery products who will buy Detergents_Paper and Milk products. Delicatessen seems unrelated to other products.

Clustering with Agglomerative Clustering

Agglomerative Clustering algorithm groups similar objects into groups called clusters. It recursively merges the pair of clusters that minimally increases a given linkage distance. It starts with many small clusters and merge them together to create bigger clusters.

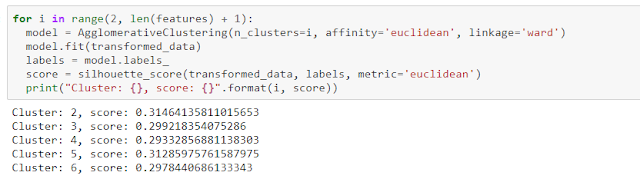
What is the number of cluster to be considered as a good parameter to algorithm for this case? Using sklearn.metrics.silhouette_score to calculate the distance between features and clusters. We choose the value with the highest score

Clearly, Model returns the highest score with cluster=2. Fitting model with data which is transformed and plotting clustered data

Channel & Products Distribution

KMeans - Clustering Method Part 1

1. What is Clustering?

Clustering is a classic machine learning problem where we don't work with labeled data. It works directly with features in data in order to figure out the pattern or logical groups in underlying dataset.

Clustering is an example of Unsupervised Machine Learning where we setup the model to learn the structure of data. It can be used as feature engineering for supervised machine learning problems such as regression or classification.

2. K-Means

The first clustering technique we'll explore is K-Means Clustering. This is very simple, intuitive and and easy to understand. The objective is to maximize the intra-cluster similarity and minimize the inter-cluster similarity.

How does it actually work?

K-Means Clustering

- Step 1: Initialize K centroids , means for example

Repeat:

- Step 2: Assign each point to a cluster

- Step 3: Recalculate the mean for each cluster

- Step 4: Re-assign the points to clusters

- Step 5: Iterate until points are in their final clusters

If the centroids are converged, stop the process. If not, the process is repeated from step 2 to step 5

3. Model Evaluation

The easy way to evaluate the clustering models is Silhouette Score because it does not require labeled data.

It measures of how similar an object is to objects in its own cluster and how different it is from objects in other clusters. Overall Silhouette score averages Silhouette coefficient of each sample.

4. Distance Metrics

4.1 Euclidean Distance

Euclidean

- The Euclidean distance is the square root of sums of squares of pairs of values from rows or columns.

- Data normalization and missing values processing must be taken into account before using this metric

Cosine

4.2. Cosine distance

- Cosine similarity is the dot product divided by the product of lengths (where the length is the square of dot product of a row/column with itself). Cosine distance is computed by subtracting the similarity from 1.

- In calculation of dot products, missing values are replaced by means. In calculation of lengths, the contribution of a missing value equals the square of the mean plus the variance.

Euclidean vs Cosine Distance

- Euclidean is useful for coordinate based measurements and more sensitive to curse of dimensionality.

- Cosine is better for data such as text where location of occurrence is less important

4.3. Manhattan Distance

Manhattan

- It is the sum of absolute pairwise distances.

- Normalization and treatment of missing values is similar as in the Euclidean distance, except that medians and median absolute distance from the median (MAD) are used instead of means and deviations.

- For discrete values, distances are again 0 or 1, hence the Manhattan distance for discrete columns is the same as the Euclidean.

4.3 Jaccard Distance

- Jaccard similarity between two sets X and Y is defined as the size of their intersection (X ∩ Y) divided by the size of the union (X ∪ Y). Jaccard distance is computed by subtracting the similarity from 1.

- Applies to sets (like word occurrence):

• Sentence A: “I like chocolate ice cream.”
• Set A = {I, like, chocolate, ice, cream}
• Sentence B: “Do I want chocolate cream or vanilla cream?”
• Set B = {Do, I, want, chocolate, cream, or, vanilla}
• Jaccard distance(sentence A, sentence B) = 1 - ( 𝐴 ∩ B)/ (𝐴 ∪ 𝐵) = 1 - 3/9

5. Case Study

We will be using the wine quality data set for our case study. This data set contains various chemical properties of wine, such as acidity, sugar, pH, and alcohol. It also contains a quality metric (3-9, with highest being better) and a color (red or white). The name of the file is Wine_Quality_Data.

We will be using the chemical properties (i.e. everything but quality and color) to cluster the wine. Though this is unsupervised learning, it can be fun to see how our clustering results map onto color and quality.

View data file on Github

5.1. Know Your Data

- Statistical Description

Dataset has 12 columns which are continuous variable. Some columns have high standard deviation or variances, we can infer that data distribution is skewed.

Max and Min values among columns are highly different so it is necessary to perform the transformation before clustering.

- Plot Quality column vs Color column on Histogram

- Pairwise maximal correlations

The correlation matrix describes two features who have highest correlation in dataset. This matrix can be presented in the following Heatmap:

5.2. Data Preprocessing

In previous part, we found the data is skewed. Plus, min and max among variables are different. In this step, we will do the normalization and the scaling.

Scaling vs. Normalization: What’s the difference?

One of the reasons that it’s easy to get confused between scaling and normalization is because the terms are sometimes used interchangeably and, to make it even more confusing, they are very similar! In both cases, you’re transforming the values of numeric variables so that the transformed data points have specific helpful properties.

The difference is that, in scaling, you’re changing the range of your data while in normalization you’re changing the shape of the distribution of your data. Let’s talk a little more in-depth about each of these options.

By scaling your variables, you can help compare different variables on equal footing.

Data Transformation

Feature Scaling with sklearn.preprocessing.RobustScaler

This means that you’re transforming your data so that it fits within a specific scale, like 0–100 or 0–1. You want to scale data when you’re using methods based on measures of how far apart data points, like support vector machines, or SVM or k-nearest neighbors, or KNN. With these algorithms, a change of “1” in any numeric feature is given the same importance.

As a result, data range in the distribution of features is changed after the scaling

Observation:

After applying the transformation with RobustScaler, the magnitude (standard deviation) of all features looks similar now.

This can prepare for next step (K-Means clustering) because it is a distance-based algorithm, this difference of magnitude can create a problem.

Data Normalization

Feature Transformation with stats.zcore

Scaling just changes the range of your data. Normalization is a more radical transformation. The point of normalization is to change your observations so that they can be described as a normal distribution.

In general, you’ll only want to normalize your data if you’re going to be using a machine learning or statistics technique that assumes your data is normally distributed. Some examples of these include t-tests, ANOVA, linear regression

zscore should be used this case instead of boxcox because some negative datapoints lie in dataset

View Notebook of Data Exploratory Analysis on GitHub

5.3. KMeans Clustering

- Fit a K-means clustering model with two clusters.

- Examine the clusters by wine color.

- Plot the distribution of wine color and clusters on bar chart

Observation

By choosing k=2, we can see that white wine is mainly distributed in cluster 1 meanwhile, data points of red wine is mostly distributed in cluster 2. The number of data points in cluster 2 are just a half of cluster 1.

How can we select the best K value?

Hyperparameter Tuning

We have to select the best number of clusters with the help of inertia, silhouette score and distance metrics

1. Selecting Inertia with Elbow Method

• Pick range of candidate values of K (e.g. 1 to 20)

• Calculate average distance from centroid for each value

• Plot and find elbow

Now fit K-Means models with cluster values ranging from 1 to 20. For each model, store the number of clusters and the inertia value.

Plot cluster number vs inertia. Does there appear to be an ideal cluster number?

Observation

When we changed the cluster value from 1 to 2, the inertia value reduced very sharply. This decrease in the inertia value reduces and eventually becomes constant as we increase the number of clusters further.

Here, we can choose any number of clusters between 4 and 8. You must also look at the computation cost while deciding the number of clusters. If we increase the number of clusters, the computation cost will also increase. So, if you do not have high computational resources, my advice is to choose a lesser number of clusters.

2. Selecting best K with Silhouette Method

• Pick range of candidate values of K (e.g.1 to 10)
• Plot silhouettes for each value of K Ideal value of silhouette = 1
• The score runs -1 to 1. The worst value is -1 and the best value is 1. Value near 0 means clusters are overlapping. Negative values generally indicate that a sample has been assigned to the wrong cluster, as a different cluster is more similar

Observation

- The best cluster that provides the highest silhouette score is 2.

- In above KMeans, Euclidean distance is used by default to calculate the Silhouette Coefficient in KMeans if we don't specify a distance metric.

- We will experiment KMeans with some other distance metrics such as Manhattan, Cosine and Jaccard.

How do distance metrics impact on the Clustering?

3. Distance metrics

Choice of distance metric is extremely important to clustering success

Each metric has strengths and most appropriate use-cases but sometimes choice of distance metric is also based on empirical evaluation

Observation:

• The silhouette score is highest with in K = 3 and distance metric = cosine 
• The optimal cluster number is selected differently among metrics

Feature Engineering with Clustering in Classification

In this section, we are going to explore clustering as a form of feature engineering.

• Create a binary target variable y, denoting if the quality is greater than 6 or not.

• Create a variable called X_with_kmeans from data, by dropping the columns "quality", "color" from the dataset.

• Create X_without_kmeans from that by dropping "kmeans".

• For both datasets, using StratifiedShuffleSplit with 10 splits, fit 10 Random Forest Classifiers and average out the roc-auc scores.

• Compare the average roc-auc scores for the models using the kmeans clusters as a feature and the one that doesn't use it.

4) For both datasets, using StratifiedShuffleSplit with 10 splits, fit 10 Random Forest Classifiers and average out the roc-auc scores.

Compare the average roc-auc scores for the models using the KMeans clusters as a feature and the one that doesn't use it.

5) Let's now explore if the number of clusters have an effect in this improvement.

• Create the basis training set from data by restricting to float_column.
• Fit a kmeans algotihm with 20 clusters. One hot encode it and add it to the basis training set. Don't add it to the previous iteration.
• Fit 10 Logistic Regression models and compute the average roc-auc-score.

Plot the average roc-auc scores.

View Notebook of KMeans Clustering on Github